You may have heard of a famous study in 2010 by 2 nobel-prize winning economists, Daniel Kahneman and Angus Deaton at Princeton University that demonstrated a correlation between income and happiness. It made a lot of headlines at the time. If you just read the news articles, you would surely have come away with a misinterpretation of the data on how income correlates to happiness. In fact, nearly every time I’ve heard the study cited, the basic takeaway message was wrong if not misleading.
2010 Study: Emotional Well-Being vs Life Satisfaction
Here’s the understanding most of the public came away with: Beyond a salary of $75,000, more income has very little impact on happiness. The actual study though is far more interesting but also far more nuanced. Here’s the basics:
- Kahneman and Deaton analyzed a big data set: 450,000 responses to daily Gallup polls conducted in 2008 and 2009.
- They basically differentiated between two types of happiness: “emotional well-being vs “life satisfaction”
- Emotional well-being is the sort of happiness that one experiences on a moment to moment basis – its based on asking someone how they are feeling from one moment to another.
- Life satisfaction is the sort of happiness described by the person when they rate how they view their life as a whole.
- Kahneman and Deaton found that emotional happiness does plateau passed an income of around $75K (in 2010 or ~$105K in 2023)
- Life satisfaction however, continued to increase even beyond $75K and did not appear to plateau
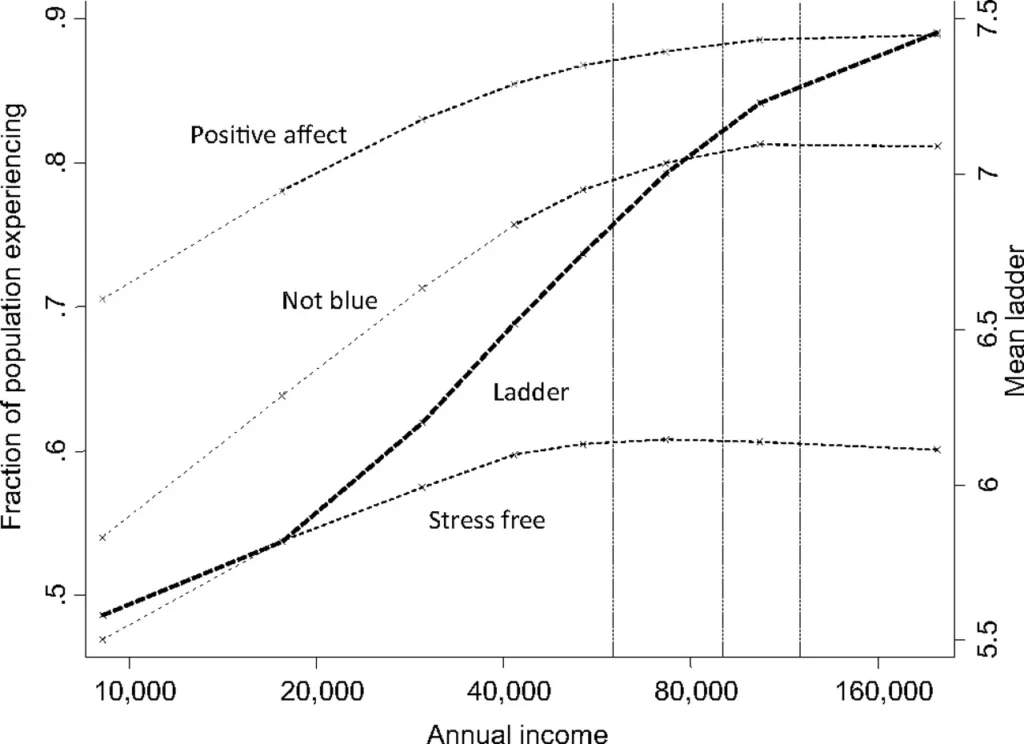
Positive affect, blue affect, stress, and life evaluation in relation to household income. Positive affect is the average of the fractions of the population reporting happiness, smiling, and enjoyment. “Not blue” is 1 minus the average of the fractions of the population reporting worry and sadness. “Stress free” is the fraction of the population who did not report stress for the previous day. These three hedonic measures are marked on the left-hand scale. The ladder is the average reported number on a scale of 0–10, marked on the right-hand scale.
2021 and 2023 Study Shows Happiness Does Increase with Income
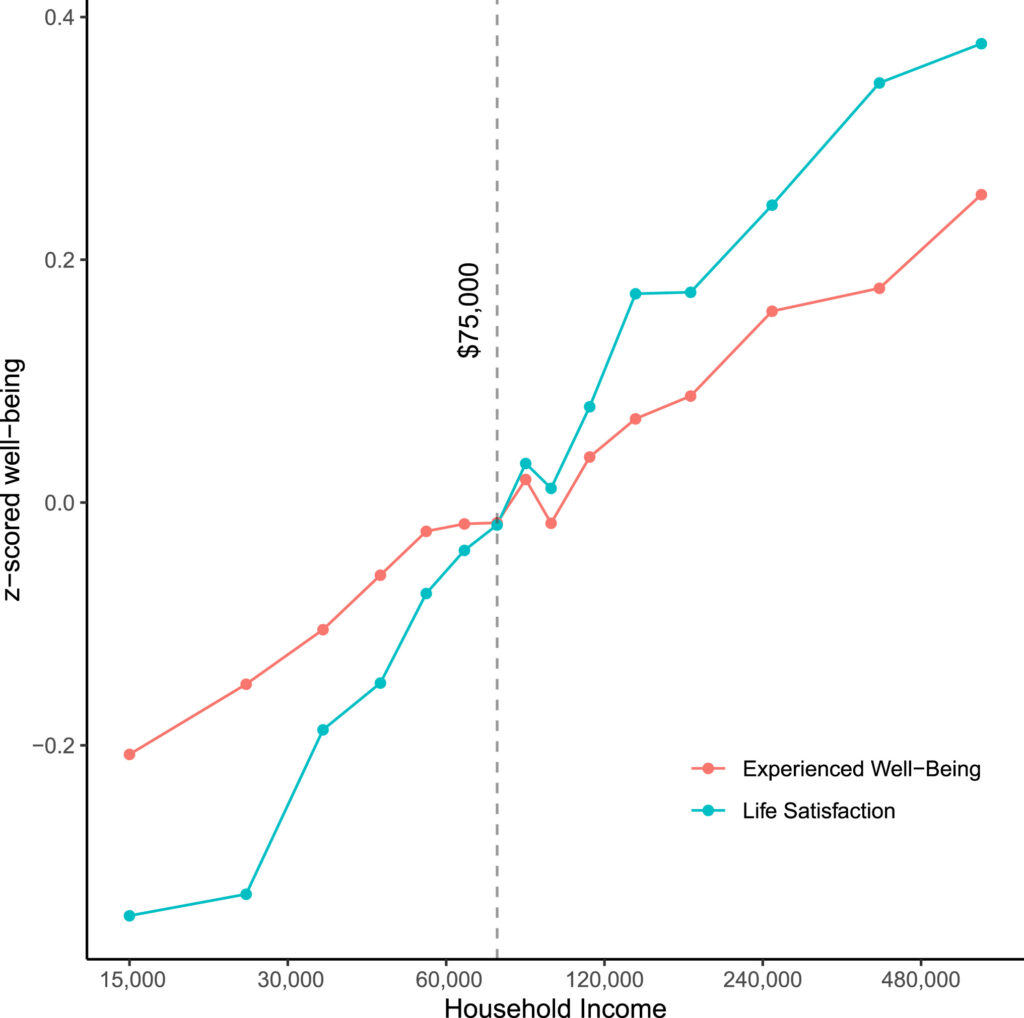
A more recent 2021 study by University of Pennsylvania senior fellow Mathew Killingworth contradicts the earlier findings by Kanheman and Deaton. Using real time data (with over a million data points) to track mood in contrast to asking people to recall their moods (as done in the 2010 study), Killingworth finds that both life satisfaction and emotional well-being continue to increase without plateauing passed the $75K mark (see the graph at the top).
Happily, the disputed finding among these renowned researchers have now been resolved in an “adversarial collaborative” paper published in March 2023 by Kanheman and Killingsworth. Essentially, Kanheman in a reversal largely agrees with Killingsworth that both life satisfaction and emotional wellbeing continue to increase beyond $75K (though less so among those who are the least happy).
Why Does Happiness Increase Beyond $75K
Note that in all the graphs above, income on the x-axis is represented logarithmically (not linearly) – so equally spaced points represent a doubling of income. That means that a large increase in income only increases happiness by a little. Whereas a $20K increase in income makes a huge impact on a person making $20K per year, that same incremental increase has very little (but not zero) impact a person making say $150K or more per year.
There’s more to the story though. Why does happiness continue to increase even after our basic needs are met? That answer is interesting and I wrote about it in a previous blog:
- As it turns out the answer is not necessarily because of anything that money buys but rather what money provides.
- University of California, Davis psychology professor Sonja Lyubomirsky explains that the wealthy tend to have greater social status, more leisure time, more fulfilling work, access to better health and nutrition, and greater security, autonomy, and control.
- Now, compare a wealthy person with a person who has achieved financial freedom (or no longer depends on their employer for their income) and what do you discover relative to these factors? Well, except for the ability to acquire more possessions (which due to “hedonic adaptation” does not have much impact on our happiness), there is a lot of overlap.
- Those who achieve financial freedom also have more leisure time, can choose the sort of work that is fulfilling for them, achieve financial security, and have greater autonomy and control. While the wealthy person may still hold greater social status, there are other non-monetary goals that those who are financially free may pursue that make up for that in other ways.
- All said, there is ample reason to think that financial freedom– as opposed to becoming fabulously wealthy– provides much of the same level of benefits that studies have found correlated with higher incomes.
Here’s the point: although trying to make more money for the purpose of social comparison may make us a bit happier on the margins, we’ll gain much greater happiness if we aim for financial freedom instead. In other words, aiming to be free of consumerism provides a shortcut that “pays off” in a big way.

Why the Dollar Figures are Inflated (my opinion)
There’s another point to be made here. I’m not an expert in the area of happiness economics so I’m sure to invite criticism here but I seriously doubt the relevance of the income findings with respect to happiness that I don’t hear addressed anywhere. I want to make clear though that this is just my opinion. I have rationale to back up what I claim but no specific data that I can point to. Take it for what it’s worth.
Here’s the issue. Nearly all of us (and I am no exception) mindlessly overconsume and not by just a little. If you read any of my blogs/writings on air conditioning or chairs or utensils, you know what I mean. We’ve long ago accepted these as standards without which one would be hard pressed to even be considered poor – rather they are likely to be labelled as living in extreme poverty.
Now if you examine a large population of people as Kanheman, Deaton, and Killingsworth have done, and over 99% of them mindlessly overconsume (admittedly this is an estimate I came up with) to simply keep up with ever increasing societal standards of living, then many of us are bypassing the shortcut: by embracing the philosophy that the best things in life are free and investing the remaining income, we can become financially independent of our employer and enjoy many of the benefits that the wealthy receive today.
Instead, the vast majority of us are taking a convoluted circuitous route to happiness. In other words, there is something problematic about all these studies and that problem lies in the behavior of the population being studied.
Notably, the 2021 study by Killingsworth showed a log-linear correlation all the way to $500K. Beyond that level of income, data was limited and so conclusions could not be drawn. This is significant to me because I know people who make that much money in a year. They do what just about everyone I know does, they spend right up to the limits of their income. Yes, they do have some more saved (and so it makes sense they can sleep better at night and meet unexpected expenses) but most of them are still dependent on their employers for their income. Very few of them are actually financially independent.
It’s not that $75K or $500K has any true relevance in my opinion. It’s that nearly all of us are over-consuming by a large amount and spending close to our income limit. So, cut out all the mindless consumption and that threshold beyond which income impacts happiness would likely drop significantly. I’m interested in seeing a study comparing those who are financially independent vs making $500K a year but still dependent on their employers. Let’s see how their levels of happiness compare.
BOTTOM LINE: THERE IS A BETTER WAY!
- As John Maynard Keynes said a century ago, people of our time ought to be largely independent of our employers for our income – unfortunately, due to “mindless consumerism”, we are not.
- Mindless consumerism is the underlying reason leading to the rise of chronic disease for 3 major reasons:
- It ties us to dependence on our employers and modern day employment is a health hazard for most (in part due to the sedentary nature of most jobs).
- It has led to environmental changes toxic to our wellbeing:
- (a). We evolved in and are best suited to natural environments and instead we live in increasingly artificial environments.
- (b). Overconsumption has lead us to engineer out the need for meaningful use of our legs for ambulation.
- Finally, it transforms workers to work with blinders on – instead of working for the product or service and receiving money as a side effect, workers focus on making money and the product or service is instead the side effect. The results (with respect to health) is that “food” is no longer food but changed to maximize pleasure and extract profit in spite of the toxicity to our health.
- Based on the science of wellbeing one can derive the philosophy that once basic needs are met, “The best things in life are free” therefore —>
- Most people can live far below their means without sacrificing happiness AND by investing the rest, they can become financially independent of their employers enabling them to be —>
- Happier. Healthier. Wealthier. More engaged. Simply better.

